A picture frame that lost a staple or other fastener can shift of out square, like the one on the right. The picture doesn’t fit and the backing shows through. With some old fashioned math and a new fastener, make this off-kilter frame perfect again.
Pencils in a Basket by Public Domain Pictures.Net Circled Pencils by Stux
Square 90 Degree Corners the Easy Way
Many home repair and remodeling projects require you to keep square corners square. A square corner has a 90-degree angle. A perfect square or rectangle has four corners that each measure 90 degrees. If the corner angles shift away from 90 degrees, the shape becomes a parallelogram.
Pre-hung interior doors or picture frames like those above are good examples and fairly simple projects that virtually any homeowner could undertake by themselves. Both require square corners.
In the out-of-square picture frame above, the upper left and lower right corners are less than 90 degrees. High school geometry taught us that a square or a rectangle has four 90 degree corners with opposite sides parallel.
Equal diagonal measurements of a square or rectangle will verify that the corners are right angles or 90 degrees. In the picture to the left, the square has four equal sides and each corner is 90 degrees, or a right angle. If you draw a line from one corner to the opposite corner, the square or rectangle turns into two right triangles. A line drawn between other two corners will be exactly the same length if the corners are 90 degrees.
Measure from A to C and from B to D. If the two measurements are equal, all the corners are 90 degrees. If one diagonal is longer than the other, as in the picture frame on the left above, the frame is out of square. The corners with the longer diagonal measurement are smaller than 90 degrees, and the other two corners are larger than 90 degrees.
This makes it easy to determine if any rectangular frame is square or needs adjustment.
The Trick
If the two diagonal measurements are not equal, just move one of the corners on the longer diagonal toward one of the corners on the shorter diagonal until both measurements are equal.
Look at the picture frame above on the left. The longer diagonal is from upper left to lower right. Move the lower right corner up and each frame corner becomes a 90 degree square when both diagonals have the same length.
Make it Easier
You could measure both diagonals repeatedly until both are equal. This tends to turn into a frustrating dance of trial and error that takes a lot of time, especially when you’re dealing with a door or window frame that you want as perfect as possible. We can simplify by determining what the diagonal measurement should be in the first place. We do this using the Pythagorean Theorem from geometry. The length of the diagonal side of any right triangle is the square root of the sum of the squares of the two sides. Put simply, side A squared + side B squared = side C squared or A2 + B2 = C 2. In the rectangle shown, we can easily calculate the expected length of the diagonal with virtually any calculator. Assume side A is 10 units, and side B is 9 units.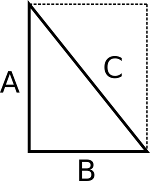 A2 = 10 x 10 = 100.
B2 = 9 x 9 = 81.
A2 + B2 = 100 + 81 = 181.
C2 = 181.
C = √ 181.
C = 13.45.
A2 = 10 x 10 = 100.
B2 = 9 x 9 = 81.
A2 + B2 = 100 + 81 = 181.
C2 = 181.
C = √ 181.
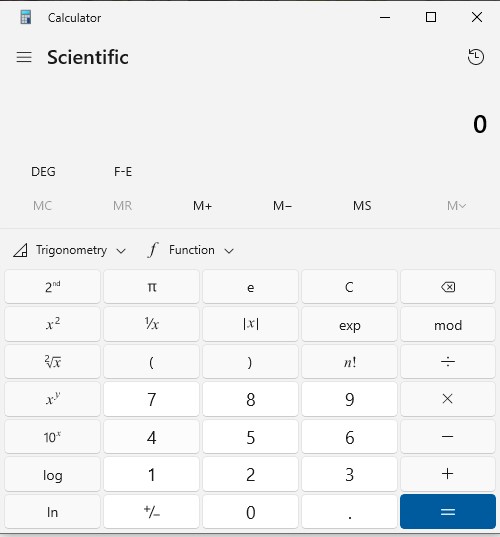
C = 13.45.Use a Calculator
Enter the length of Side A: 10 (Length of A)
Press X2 and the display reads 100 (A2 = 10 x 10 = 100)
Press +
Enter the length of Side B: 9 (Length of B)
Press X2 and the display reads 81 (B2 = 9 x 9 = 81)
Press = and the display reads 181 (A2 + B2)
Press √ to display the answer 13.45362404707371031716308546217
You don’t need all those numbers. Just round it off to two or three digits or 13.45
Now the Square Corners with 90 Degree Angles are Easy
No need to measure multiple times to get it perfect. Now you know the distance between opposite corners must be 13.45. Hold your tape measure or other measuring tool across two opposite corners. Move the sides until the measure reads 13.45. If you measure the other side, it will read 13.45 also.
Many of us in the USA use good old inches and feet to measure things. That’s fine and it is what we are used to. At least, until you’re scratching your head trying to figure out what fraction on your tape measure corresponds to 13.45.
The really great thing about this math is that it works for any measurement system from inches or feet to parsecs, astronomical units, or… meters, centimeters, and millimeters.
100 centimeters (cm) = 1 meter (m).
10 millimeters (mm) = 1 centimeter (mm).
If you measured in centimeters or millimeters, you wouldn’t worry about that fraction at all. You’d just adjust the frame diagonal to 134.5 mm and be done. No conversion. No anything. Just measure everything millimeters and be done with it.
If you’re still stuck on your fractions, 13.45 is almost, but not quite equal to 13 29/64. Be sure to wear your reading glasses to see those 1/64 marks on your tape rule.
